| Plant Maintenance Resource Center
Measure Field Reliability with Statistics
|
||
|
|
|
|
|
Measure Field Reliability with StatisticsAuthor: Larry George Statistics convert data into actionable information, information that helps you decide whether to do anything and what to do, to what, when, and how much. This information can save half of your field service costs, double profit from service, or have unexpected consequences that companies don't disclose. Misunderstandings about what reliability is and which data is necessary to measure it limit the value of reliability statistics. This article describes reliability prediction and estimation from data required by generally accepted accounting principles. Blanchard says reliability is "the probability that a system or product will perform in a satisfactory manner for a given period of time when used under specified operating conditions." The military standard definition of reliability is, "the probability that an item will perform a required function without failure under stated conditions for a stated period of time." Probability has stood the test of time as a useful measure of survival randomness, so reliability is P[Life > age] for ages within the useful product life, whether for hardware, electronics, or humans. The time variable is age for most products, whether in calendar hours or operating hours, miles, cycles, etc. As far as customers are concerned, the only appropriate operating conditions are field conditions, not in a laboratory. Reliability is not MTBF. Reliability engineers and their managers believe they have to test to measure reliability. Have you ever said, "We need to test at least n units for at least t hours to verify P[R > .95] > .9"? You figure out the smallest n and t you can possibly test (http://www.sre.org/sresoft.htm). Then your manager says you can test only half as many units for half the time. Typically, n and t are based on an incorrect constant-failure-rate assumption, thereby eliminating any chance of learning actionable information. (A constant failure rate implies the absence of infant mortality, wearout, and the need for maintenance). People believe that it is necessary to track at least a sample by serial number from birth to death to estimate field reliability. This data gives ages at failures and survivors' ages, which are sufficient but not necessary. Most companies have given up tracking parts by serial number because of errors, data storage requirements, and failure to use actionable reliability information. Fortunately, tracking parts by serial number is not necessary for either field reliability prediction or estimation. Reliability Prediction?People make MTBF predictions, argue about them, and compare lies. "My MTBF is bigger than yours." Most MTBFs are predictions, seldom verified. They are predictions of averages, not age-specific reliability. Have you seen predictions in the range of 500,000 hours for computer hardware? That's 250 years for a computer operated 2000 hours per year, M-F, 9-4, or more than 50 years for continuous operation. To predict age-specific field reliability, use field reliability of comparable products. Designs may change, but other factors (process, environment, and customers) that determine field reliability don't. The field reliability of comparable products provides a reasonable, relative reliability prediction. Scale the fielded products' age-specific failure rates to take changes in MTBF predictions into account to make an age-specific reliability prediction [George and Langfeldt]. Alternatives to Test and MTBF PredictionIt is a waste of time and credibility to track annual failure rate (AFR) and argue about wiggles in monthly AFR charts. AFR, annual returns divided by the installed base, is an average and provides little actionable information, too late, and too imprecisely. It is a waste of talent, ability, and initiative not to use actionable information from available data. Several clients have asked for age-specific reliability predictions, because their customers asked. They wanted to know the probability of being dead on arrival, the probability of failure in the first month, first three months, six months, year, etc. Age-specific reliability predictions provide actionable information because, although designs change, age-specific reliability doesn't change, much. Designs change, but manufacturing, packaging, shipping, installation, environment, and customers don't. Until there's field experience with new products, age-specific reliability predictions help plan warranty, service, spares production, and burn-in and assist the designers. It's not necessary to track products and parts by serial number to estimate age-specific reliability. Tracking parts by serial number requires about 1000 times as much data storage capacity and probably incurs more than 1000 times as many errors, compared to ships and returns data (table 1). Generally accepted accounting principles require ships and returns data, which is sufficient for estimating age-specific reliability. That means that your company has sufficient data [George]. Ships and returns are population data, so reliability estimates from them have no sample uncertainty.
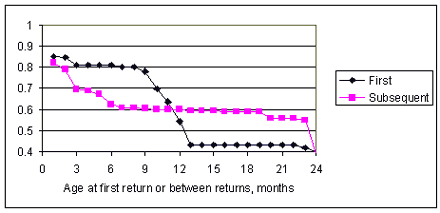
Figure 1 shows the field reliability estimated from the ships and returns data in table 1. It shows two reliability functions, one for the age at first warranty return and one for the age between subsequent returns. The probability of drivetrain's being returned in the first month was more than 15% initially and 18% subsequently. The former indicates that many were defective practically from delivery. The latter indicates that the problems didn't get fixed. The 1988 Ford V-8-460-cubic-inch engine was the last Ford engine with a carburetor, a very unhappy engine.
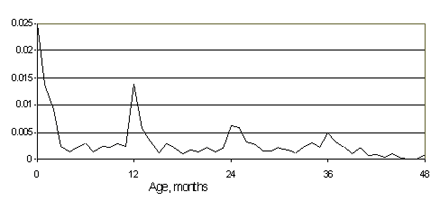
Age-specific failure rates help failure analysisThe failure rate function shows what's happening (see figure 2). Process defects cause infant mortality, evidenced by an initially decreasing failure rate. Design defects cause prematurely increasing failure rates. Other phenomena, such as warranty expiration anticipation, preventive maintenance, and periodic inspections, also manifest themselves.
Engineers regard design defects as more significant than process defects.They assume that their designs will be produced, packaged, shipped, installed, and operated in a manner that achieves inherent reliability. Design defects cause premature wearout, which becomes apparent pretty early in the product life cycle, although not as early as process defects, which cause infant mortality. Engineers should be reassured to know that, for most products, retirement occurs before wearout, so the failure rate function decreases with age. ConclusionDon't give up on statistics, even for reliability predictions. Population statistics eliminate sample uncertainty and help you predict, measure, and use age-specific field reliability, without tracking parts by serial number. Which do you prefer, randomness with uncertainty or without? Uncertainty means you're gambling without knowing the odds. References
Larry George is an ASQ Certified Reliability Engineer. He has a Ph. D. in industrial engineering and operations research, with a minor in statistics. He taught for 11 years, worked for a national laboratory for 11 years, and has worked in the real world for more than 20 years. ASQ just elected him as a Fellow. Contact him at pstlarry@yahoo.com. Copyright 1996-2009, The Plant Maintenance Resource Center . All Rights Reserved.
|